Direct Proportionality in a Spec
So, you're asking, what did all that have to do with spectrophotometers?
Good question. Here's the short answer: a spectrophotometer is a device that measures how much light a solution absorbs, which is DIRECTLY PROPORTIONAL to the concentration of the solution.
That was a
bit dense. Let's try a longer answer (stay with me here...): If you don't clean a fish tank for a
long time, the water gets murky, right? That happens because lots of stuff (bacteria, algae, waste
products) is floating around. And how can you tell lots of stuff is floating around? Because it's
hard to see through. In a really bad case, you can't even find the fish. So, stuff floating around
means light can't get through the water.
What if you could figure out a relationship between how much light gets through and how much stuff is floating around? Then you would have an easy way to figure out how badly off your fish are. Instead of taking a water sample, adding chemicals to preserve the cells, putting it under a microscope, and counting hundreds of tiny cells, you could just shine a light through it and measure how much light came out!
This is exactly what a spectrophotometer does. You take a solution, figure out what wavelength of light is most useful (more on that in a sec), then shine that light through and record how much got absorbed. Finally you use a graph like the one below to "translate" how much light got absorbed into how much stuff was in the water (officially, to "find the concentration of the solution").
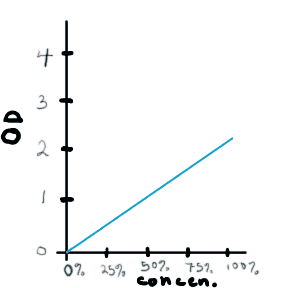
Wow, cool, notice the DIRECTLY PROPORTIONAL relationship here.
- No gunk, no light absorbed.
- A little gunk, a little light absorbed.
- Lots of gunk, lots of light absorbed. Bye bye fish.
What is the slope of the graph above?
Before you can even start to answer this, you need to think about units. Y is measured in OD units (whatever they are... we'll get to that). X is concentration, which ranges from 0 percent to 100 percent. So a useful unit for x would be "percent concentration". Thus the units of the slope are "OD / percent concentration".
(To make this problem interactive, turn on javascript!)
- I need a hint ... : Approximately what is the value of y at x=50?
- ...another hint ... : At x = 50, y = 1, so the slope is 1/50
- ...another hint ... : 1/50 simplifies to...
I think I have the answer: 0.02 units OD/percent concentration
In other words, the OD increases by 0.02 units for every additional 1 percent concentration of gunk.
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu