MathBench > Statistics

Normal Distributions and the Scientific Method

Normal Fish

Now I want to focus a little more on the replication part of the procedure. Why do you need to replicate? Think what would happen if you treated one fish with Fish2Whale, and gave normal fishfood to one other fish. Just by chance, you might happen to pick a scrawny, weakly fish for the treatment, and a robust, strapping fish for the control. Of course you would try not to, but sometimes it's hard to tell a fish by its scales. Or, your treatment fish might happen to get the fish version of stomache flu, or fall in love, or all sorts of other things could happen that would mess up your experiment.

a hundred fish The "insurance", so to speak, is to use LOTS of treatment fish, and also lots of control fish. This is called replication. But there's a slight catch. You put lots of fish in a tank and try to treat them all the same, and feed them all Fish2Whale, but they don't all grow to be exactly the same size. In a way, that's the point -- the reason why you have to replicate is that fish DON'T react in a completely predictable manner. But still, it creates a problem. How do you summarize the growth of a hundred or so fish?

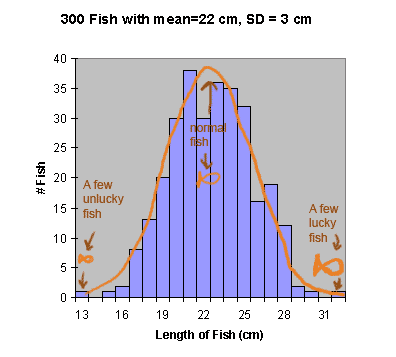
If you are lucky, the sizes of fish will be similar to what's called a "normal distribution". The reason it's called "normal" is that it is seen so often in nature that it seems like the "normal" distribution. This kind of distribution occurs when many factors influence an outcome -- for example, fish growth is affected by temperature, light, general health of the fish, ability to compete with other fish, and so on. Normally, for any given fish, some of these factors are positive and some of negative, so most fish end up close to the average. For a few fish, all the factors line up just right, and those fish get bigger than normal. For a few fish, everything or almost everything goes wrong, and those fish turn out quite small.