Calculus Man saves the day !!!
We've already talked the equilibrium idea to death, but here it is again:

Luckily for the setting-equal business, we actually have equations for both of these forces. The diffusion equation should look familiar to you:
movement of particles = P * A * ΔC
(We're just going to punt on the values of the "P" and "A" constants for the moment -- its enough to know that they are constants and not variables). The equation for the movement of charge along a charge gradient is similar, except it also has a term for the concentration (why? ask your teacher when you get to Mamm Phys):
movement of ions = g * C * ΔV
(Likewise we're not going to bother asking what the value of "g" is). So, all we need to do is set these two equations to equal in size but opposite in direction, and we'll have equilibrium:
P * A * ΔC = - g * C * ΔV
or, rearranging:
ΔV = P * A * ΔC / (- g * C)
Cool ! Well, almost. There is one big problem: we would like to get rid of the deltas, which stand for differences between timestep 1 and timestep 2. Think about it -- as soon as you open the channel, the concentrations change and the amount of voltage changes too. In other words, you are trying to track (and add up) a moving target. It might help to use very tiny timesteps. In other words, this is a job for...
Calculus-Man!
Luckily for us, Calculus-Man can leap tall equations in a single bound, giving us the following formula:

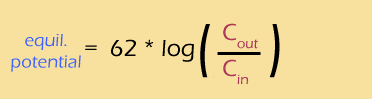
The fine print:
This formula valid only at normal body temperature and pressure. Other conditions may induce different values of the constant. Results at home may vary. Void where prohibited by law. Exchange value 1/20 ¢
The gory details (actually its not all that hard, but feel free to skip if you want):
First, we need really small timesteps, so we'll use the continuous "d" rather than the discreet "Δ". Also, we need to add up (or integrate) the changes between the outside and the inside of the membrane. So, here it is:
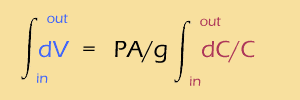
Now, one of the few integrals from Calc II that you absolutely should memorize is the integral of 1/x, which is ln(x). So,
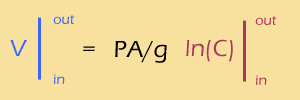
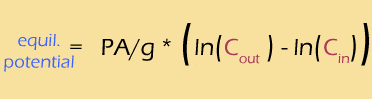
Meanwhile, the difference of logs is the same as the log of the RATIO, so
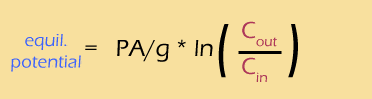
 Using a bit of pixie dust, we can substitute "log" for "ln" (this is called a "change of base", and I have to look it up every time I do it). This is a strictly cosmetic step -- the natural log works perfectly well, but the base-ten log is easier to interpret. At the same time, we'll calculate the actual value of that mess of constants, to get:
Using a bit of pixie dust, we can substitute "log" for "ln" (this is called a "change of base", and I have to look it up every time I do it). This is a strictly cosmetic step -- the natural log works perfectly well, but the base-ten log is easier to interpret. At the same time, we'll calculate the actual value of that mess of constants, to get:
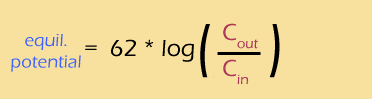
Voila, one of the few truly simple applications of integral calculus in biology!
Copyright University of Maryland, 2007
You may link to this site for educational purposes.
Please do not copy without permission
requests/questions/feedback email: mathbench@umd.edu