Table of Contents

• Section 1. Exact Doubling Time
• 1: In search of ... the exact doubling time
• 2: Finding doubling time with general numbers
• 3: Logarithms = Exponent-busters
• 4: Test your knowledge of logs
• 5: More exponent busting
• Section 2. Applications
• 6: World Population
• 7: Growth of technology
• 8: How long before the oysters are unsafe?
• Review
• 9: Summary

World Population Growth

 

Let's take a breather from rapid-onset, life-threatening illnesses for a moment. 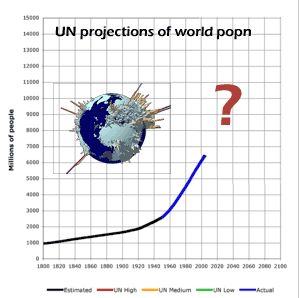Although we've been talking only about cholera, this same procedure can work to find the exact doubling time for any data. For example... how about world population, which recently topped 7 billion. How has doubling time changed over the decades?

Year	Population (in billions)
1900	1.6
1950	2.5
1999	6
2012	7

 

From 1900 to 1950, 1.6 billion became 2.5 billion. So, we write

2.5 = 1.6 * 2^n

2.5/1.6 = 2^n

log(2.5/1.6) = n*log(2)

with a bit of rearranging and calcalator punching, we find that the doubling time is

From 1950 to 1999, doubling time is

From 1999 to 2012, doubling time is

So is world population growing exponentially? Well, yes and no. If you look at the graph of population size over the last 100 years, it certainly shows an upward curve that makes us think of exponential growth. However, the growth factor is NOT constant -- we know that because we showed that doubling time decreased from 78 to 39 years over the 1900's. So growth was actually FASTER than exponential.

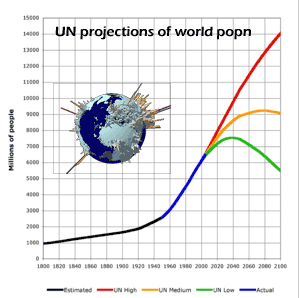
What about the current century? Doubling has decreased to almost 60 years, so growth is slowing down. We could still say it is exponential, but at a lower rate. In fact, the UN "medium" population prediction is that world population would top out between 9 and 10 billion people within the next 100 years.