Table of Contents

• Prequiz...
• 1: Osmosis is a special kind of diffusion
• 2: Putting the Os into Osmolarity
• 3: Calculating osmolarity
• 4: Osmolarity adds up
• 5: Which way will water flow?
• 6: ...and how fast?
• 7: What else can the equations tell us?
• 8: Where does it all end?
• 9: Drink your water
• 10: Sharks, alligators, and goldfish
• Review
• 11: Summary

Learning Outcomes

After completing this module you should be able to:

• Determine the osmolarity of a solution.
• Use a two-compartment model to determine which way water will flow through a selectively permeable membrane, and the rate of flow of water.

Osmosis is a special kind of diffusion

First we told you that diffusion through a membrane was just a special case of diffusion -- we were able to assume that there were only two compartments of interest (left and right), which simplified the maths a lot.

 

Now, we're going to tell you that osmosis is a special case of diffusion through the membrane. It's the membrane that makes it special. Recall that membranes vary in terms of their permeability. Some might be like the proverbial brick wall, while others might be 'as leaky as a sieve'. Imagine a membrane with gaps* just big enough to let water through, but too small to let anything else across.

 

How is this a special case of diffusion through a membrane? Basically, what happens is that water can diffuse through the membrane, but nothing else in the water -- salt, sugar, or other solute -- can.

 

Instead of general permeability of the membrane, what we care about now is permeability to water, or P_water .

Continuous form
Discrete form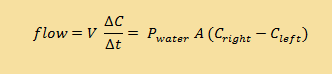

 

*More properly, permeability of the membrane has to do with selective gateways and polarity and so on, but imagining gaps in the membrane will work too.

Clipart for this module thanks to Arthur's Clipart, FreeImages.co.uk, Clipart Heaven